I. Introduction
L'eau peut-elle allumer des bougies ? C'est vrai !
Est-il vrai que les serpents ont peur du réalgar ? C'est faux !
Ce dont nous allons parler aujourd'hui, c'est :
Les interférences peuvent-elles améliorer la précision des mesures ?
En temps normal, les interférences sont l'ennemi naturel des mesures. Elles réduisent la précision des mesures et, dans les cas les plus graves, les rendent impossibles à réaliser correctement. Par conséquent, affirmer que les interférences peuvent améliorer la précision des mesures est une idée fausse !
Cependant, est-ce toujours le cas ? Existe-t-il une situation où les interférences n’altèrent pas la précision de la mesure, mais l’améliorent au contraire ?
La réponse est oui !
2. Accord d'ingérence
Compte tenu de la situation actuelle, nous parvenons à l'accord suivant concernant l'ingérence :
- Les interférences ne contiennent pas de composantes continues. Lors de la mesure, il s'agit principalement d'interférences alternatives, ce qui est une hypothèse raisonnable.
- Comparée à la tension continue mesurée, l'amplitude des interférences est relativement faible, ce qui correspond à la réalité.
- Une interférence est un signal périodique, ou dont la valeur moyenne est nulle sur une période donnée. Ce point n'est pas nécessairement vérifié lors de mesures réelles. Cependant, comme l'interférence est généralement un signal alternatif de fréquence plus élevée, la convention d'une moyenne nulle reste raisonnable pour la plupart des interférences sur une période plus longue.
3. Précision de mesure en présence d'interférences
La plupart des instruments et compteurs électriques utilisent désormais des convertisseurs analogique-numérique (CAN), et leur précision de mesure est étroitement liée à la résolution de ces convertisseurs. En règle générale, les CAN à haute résolution offrent une meilleure précision de mesure.
Cependant, la résolution d'un convertisseur analogique-numérique (CAN) est toujours limitée. En supposant une résolution de 3 bits et une tension de mesure maximale de 8 V, le CAN est équivalent à une échelle divisée en 8 divisions, chacune correspondant à 1 V. Le résultat de la mesure est toujours un entier, et la partie décimale est systématiquement reportée ou supprimée (reportée dans cet article). Ce report ou cette suppression entraîne des erreurs de mesure. Par exemple, 6,3 V est supérieur à 6 V et inférieur à 7 V. Le résultat de la mesure du CAN est de 7 V, soit une erreur de 0,7 V. Cette erreur est appelée erreur de quantification du CAN.
Pour faciliter l'analyse, nous supposons que l'échelle (convertisseur AD) ne présente aucune autre erreur de mesure que l'erreur de quantification AD.
Nous utilisons maintenant deux balances identiques pour mesurer les deux tensions continues représentées sur la figure 1 sans interférence (situation idéale) et avec interférence.
Comme le montre la figure 1, la tension continue mesurée est de 6,3 V. La figure de gauche, exempte d'interférences, présente une valeur constante. La figure de droite illustre la perturbation du courant continu par le courant alternatif, ce qui se traduit par une certaine fluctuation. Après élimination des interférences, la tension continue du diagramme de droite est égale à celle du diagramme de gauche. Le carré rouge représente le résultat de la conversion analogique-numérique.

Tension continue idéale sans interférence
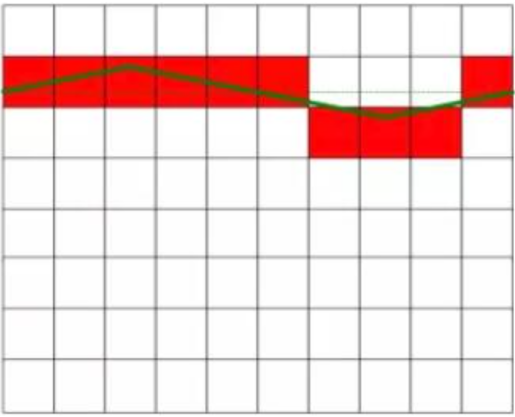
Appliquez une tension continue parasite de valeur moyenne nulle.
Effectuez 10 mesures du courant continu dans les deux cas de la figure ci-dessus, puis calculez la moyenne des 10 mesures.
La première échelle à gauche est mesurée 10 fois, et les valeurs sont identiques à chaque fois. En raison de l'erreur de quantification du convertisseur analogique-numérique, chaque mesure est de 7 V. Après le calcul de la moyenne des 10 mesures, le résultat est toujours de 7 V. L'erreur de quantification du convertisseur analogique-numérique est de 0,7 V, et l'erreur de mesure est également de 0,7 V.
La deuxième échelle à droite a considérablement changé :
En raison de la différence entre la tension d'interférence (positive ou négative) et son amplitude, l'erreur de quantification du convertisseur analogique-numérique (CAN) varie selon les points de mesure. Sous l'effet de cette erreur, la tension de mesure oscille entre 6 V et 7 V. Sept mesures ont donné 7 V, trois seulement 6 V, et la moyenne des dix mesures est de 6,3 V ! L'erreur est donc nulle.
En réalité, aucune erreur n'est impossible, car dans le monde objectif, il n'existe pas de tension de 6,3 V stricte ! Cependant, il en existe bel et bien :
En l'absence d'interférence, puisque chaque résultat de mesure est identique, après avoir fait la moyenne de 10 mesures, l'erreur reste inchangée !
En présence d'une interférence suffisante, après moyennage de 10 mesures, l'erreur de quantification du convertisseur analogique-numérique est réduite d'un ordre de grandeur ! La résolution est améliorée d'un ordre de grandeur ! La précision de mesure est également améliorée d'un ordre de grandeur !
Les questions clés sont :
Est-ce la même chose lorsque la tension mesurée prend d'autres valeurs ?
Les lecteurs pourront suivre l'accord sur les interférences de la deuxième section, exprimer les interférences par une série de valeurs numériques, superposer les interférences à la tension mesurée, puis calculer les résultats de mesure de chaque point selon le principe de report du convertisseur AD, puis calculer la valeur moyenne pour vérification, tant que l'amplitude des interférences peut entraîner un changement de la lecture après quantification AD, et que la fréquence d'échantillonnage est suffisamment élevée (les changements d'amplitude des interférences ont un processus de transition, plutôt que deux valeurs positives et négatives), et la précision doit être améliorée !
Il est possible de démontrer que tant que la tension mesurée n'est pas un entier (ce qui n'existe pas dans le monde objectif), une erreur de quantification du convertisseur analogique-numérique (CAN) se produira. Quelle que soit l'ampleur de cette erreur, si l'amplitude de l'interférence dépasse l'erreur de quantification ou la résolution minimale du CAN, la mesure oscillera entre deux valeurs adjacentes. L'interférence étant symétrique (positivement et négativement), son amplitude et sa probabilité de diminution et d'augmentation sont égales. Par conséquent, plus la valeur réelle est proche d'une valeur donnée, plus la probabilité d'observer cette dernière est élevée, et c'est cette dernière valeur qui sera la plus proche après moyennage.
Autrement dit : la valeur moyenne de plusieurs mesures (la valeur moyenne d’interférence est nulle) doit être plus proche du résultat de mesure sans interférence, c’est-à-dire que l’utilisation du signal d’interférence AC avec une valeur moyenne de zéro et la moyenne de plusieurs mesures peuvent réduire les erreurs de quantification AD équivalentes, améliorer la résolution de mesure AD et améliorer la précision de la mesure !
Date de publication : 13 juillet 2023




